
When we run the analysis, we reuse the previous regression command, we just add gle_rgdpcafter p_polity2. But will there remain a relationship between democracy and life expectancy? Regression analysis with a control variable ¶īy running a regression analysis where both democracy and GDP per capita are included, we can, simply put, compare rich democracies with rich nondemocracies, and poor democracies with poor nondemocracies. The main relationship will also become more positive if we control for a variable that has a negative correlation with the dependent variable, and a positive correlation with the independent. It is thus likely that the relationship between democracy and life expectancy will weaken under control for GDP per capita.Ĭonversely, if we control for a variable that has a positive correlation with the dependent, and a negative correlation with the independent, the original relationship will become more positive. The same is true if we control for a variable that has a negative correlation with both independent and dependent. When we control for variables that have a postive correlation with both the independent and the dependent variable, the original relationship will be pushed down, and become more negative. This relationship is very strong, 0.63, considerably more than the relationship between democracy and life expectancy (0.29). High GDP per capita is also associated with higher life expectancy. Democratic countries are thus richer, on average. More GDP per capita is associated with more democracy, and and more democracy is associated with more GDP. The relationship between democracy p_polity2 and GDP gle_rgdpc is 0.15. In this matrix we find three relationships, standardized according to the Pearson's R measure, which runs from -1 (perfect negative relationship) to +1 (perfect positive relationship), via 0 (no relationship). A standard measure of that is GDP per capita:
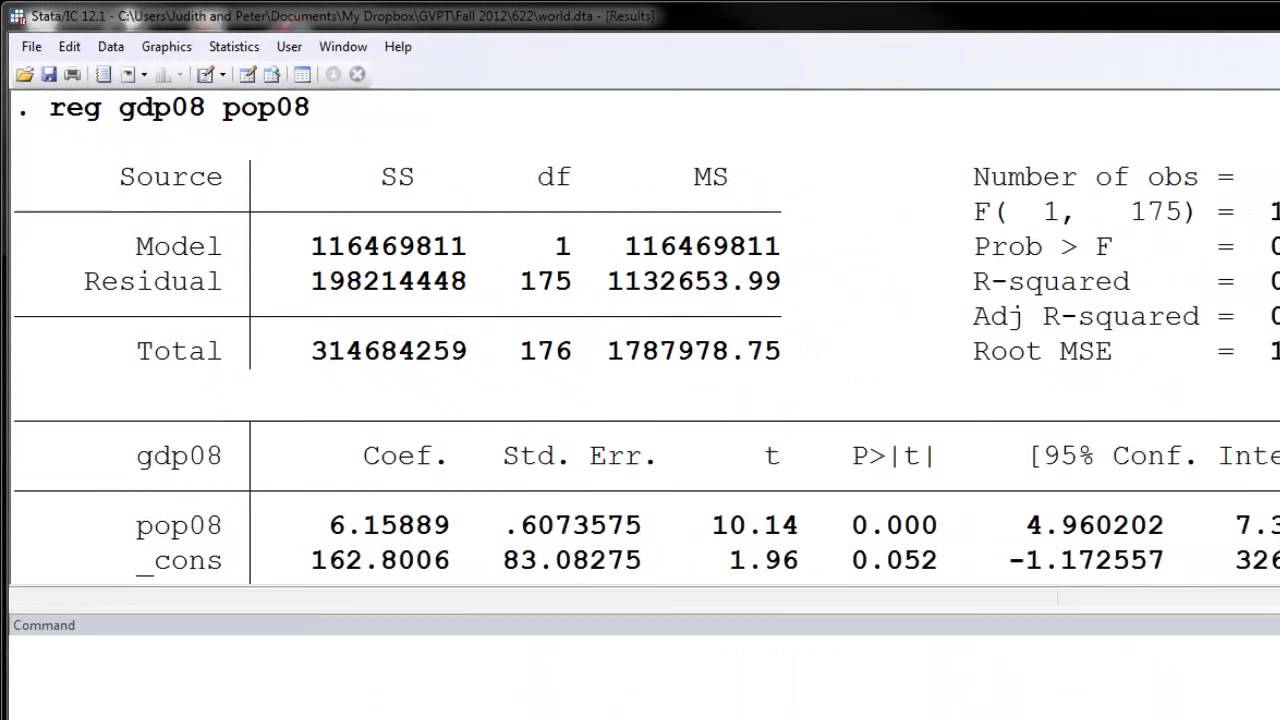
To test the hypothesis that democracy leads to longer life expectancy, we will control for economic development. Richer countries can also invest more in health care and disease prevention, for instance through better water supply and waste management. Democracy research shows that countries with more economic prosperity are more likely to both democratize and keep democracy, once attained. Controlling for a variable ¶Īn obvious suspect is the level of economic development.

Democracy and life expectancy might be two symptoms, rather than cause and effect. There might be other factors that lead to both democracy and high life expectancy. This explains the low R squared value.īut does this positive relationship mean that democracy causes life expectancy to increase? Not necessarily. But we can also see that the line is not a great fit to the dots - there is considerable spread around the line. The red regression line slopes upward slightly, which the regression analysis also showed (the b-coefficient was positive).
Multiple regression stata how to#
In this guide I will show how to do a regression analysis with control variables in Stata. Had there been a relationship between height and speed even under control for gender, this would still not have implied that the relationship was causal, but it would at least have made it more less unlikely. And if we actually run this analysis (which I have!) we will see that no relationship between height and time remains. What we are looking at is whether tall women run faster than short women, and whether tall men run faster than short men. To "control" for the variable gender in principle means that we compare men with men, and women with women. If we don't account for the runners' gender, we would not pick that up. On average, men are taller than women, and they also have other physiological properties that make them run faster. If this was a causal relationship - for instance because you can run faster if you have long legs - we could encourage tall youth to get into track and field.īut it would be unwise, without taking other relevant variables into account variables that can affect both height and running speed. It is actually a quite strong relationship. We will then find that taller persons ran faster, on average. For data we take all the times in the finals of the 100 meters in the Olympics 2016.

Imagine that we want to investigate the effect of a persons height on running speed. And at the very least, we can investigate whether a relationship is spurious, that is, caused by other variables. However, we can make it more or less likely. No statistical method can really prove that causality is present. You've probably heard the expression "correlation is not causation." It means that just because we can see that two variables are related, one did not necessarily cause the other. A major strength of regression analysis is that we can control relationships for alternative explanations.


 0 kommentar(er)
0 kommentar(er)
